Lesson 2.6 special angles on parallel lines – Embark on an enlightening journey into lesson 2.6: special angles on parallel lines. Delve into the captivating realm of geometry, where lines intersect and angles whisper secrets. This lesson unveils the intricate relationships between corresponding angles, alternate interior angles, and consecutive interior angles, empowering you to decipher the mysteries of parallel lines with newfound clarity.
Prepare to unravel the theorems that govern these special angles, unlocking the ability to conquer geometry problems with finesse. Discover practical applications that extend beyond the classroom, illuminating the practical significance of special angles in our everyday world.
1. Special Angles on Parallel Lines
Parallel lines are two lines that never intersect, no matter how far they are extended. When two parallel lines are intersected by a transversal, several special angles are formed.
The most important of these special angles are corresponding angles, alternate interior angles, and consecutive interior angles.
1.1 Corresponding Angles, Lesson 2.6 special angles on parallel lines
- Corresponding angles are angles that are in the same relative position on two parallel lines.
- For example, the angles marked as ∠1 and ∠5 in the diagram below are corresponding angles.
1.2 Alternate Interior Angles
- Alternate interior angles are angles that are on opposite sides of the transversal and inside the parallel lines.
- For example, the angles marked as ∠2 and ∠6 in the diagram below are alternate interior angles.
1.3 Consecutive Interior Angles
- Consecutive interior angles are angles that are on the same side of the transversal and inside the parallel lines.
- For example, the angles marked as ∠3 and ∠4 in the diagram below are consecutive interior angles.
2. Theorems on Special Angles: Lesson 2.6 Special Angles On Parallel Lines
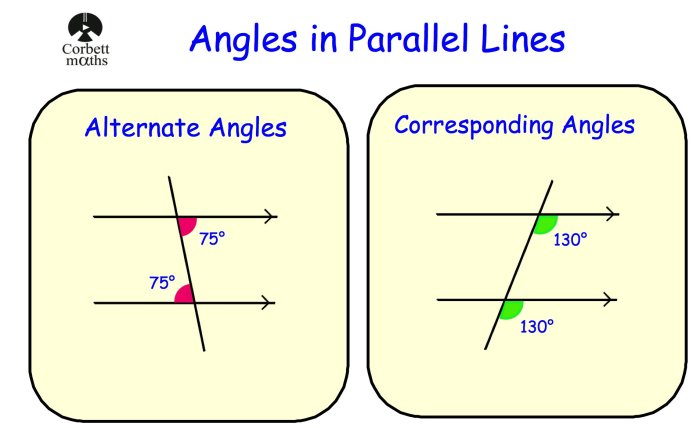
There are two important theorems that relate to special angles on parallel lines:
2.1 Theorem on Corresponding Angles
The theorem on corresponding angles states that if two parallel lines are intersected by a transversal, then the corresponding angles are congruent.
In other words, if ∠1 is congruent to ∠5, then ∠2 is congruent to ∠6, ∠3 is congruent to ∠7, and so on.
2.2 Theorem on Alternate Interior Angles
The theorem on alternate interior angles states that if two parallel lines are intersected by a transversal, then the alternate interior angles are congruent.
In other words, if ∠2 is congruent to ∠6, then ∠3 is congruent to ∠7.
3. Applications of Special Angles

Special angles on parallel lines can be used to solve a variety of geometry problems.
- For example, you can use special angles to find the measure of an unknown angle in a parallelogram or a trapezoid.
- You can also use special angles to prove that two lines are parallel.
Clarifying Questions
What is the significance of special angles on parallel lines?
Special angles on parallel lines are crucial for understanding the relationships between parallel lines and transversal lines. They allow us to determine the measure of unknown angles, solve geometry problems, and analyze geometric figures.
How can I identify corresponding angles?
Corresponding angles are angles that are located in the same position relative to the transversal and parallel lines. They are congruent and can be used to prove that lines are parallel.
What is the difference between alternate interior angles and consecutive interior angles?
Alternate interior angles are angles that are located on opposite sides of the transversal and inside the parallel lines. They are congruent and can be used to prove that lines are parallel. Consecutive interior angles are angles that are located on the same side of the transversal and inside the parallel lines.
They are supplementary and their sum is 180 degrees.